Get relevant information about Explain How To Factor When The Leading Coefficient Is 1. in this article, hopefully helping you in your information search.
In the realm of mathematics, factoring is a fundamental operation that involves breaking down complex algebraic expressions into simpler units. One particular scenario that students often encounter is factoring polynomials where the leading coefficient, the coefficient of the term with the highest degree, is 1. Understanding how to approach this scenario is crucial for solving various polynomial equations.

Explain How To Factor When The Leading Coefficient Is 1.
Let’s dive into the world of factoring polynomials with a leading coefficient of 1!
Simplifying through Combination
When factoring a polynomial with a leading coefficient of 1, one effective strategy involves combining like terms. This technique aims to group terms with the same variables and exponents. The resulting polynomial may exhibit common factors, which can then be factored out using the distributive property.
For instance, consider the polynomial x2 + 5x + 6. We can combine the like terms to obtain (x2 + 5x) + 6. Further observation reveals that the first group, x2 + 5x, shares a common factor of x. Factoring this common factor out yields (x)(x + 5) + 6.
Identifying the Roots
Factoring polynomials with a leading coefficient of 1 also involves finding the roots of the polynomial. The roots represent the values of the variable that make the polynomial equal to zero. These roots can be identified by setting the polynomial equal to zero and solving for the variable.
Continuing with our previous example, x2 + 5x + 6, we set it equal to zero: x2 + 5x + 6 = 0. Solving for x, we obtain (x + 2)(x + 3) = 0. This factorization implies that the roots of the polynomial are x = -2 and x = -3.
Utilizing the Substitution Method
Another useful technique for factoring polynomials with a leading coefficient of 1 is the substitution method. This method involves substituting possible roots into the polynomial to check if the result is zero. If a substitution makes the polynomial zero, then the corresponding value is a root, and the polynomial can be factored using that root.
For example, in the polynomial x3 – 5x2 + 6x, let’s substitute x = 2 to see if it is a root: (2)3 – 5(2)2 + 6(2) = 8 – 20 + 12 = 0. Since the result is zero, x = 2 is a root, and we can factor the polynomial as (x – 2)(x2 – 3x + 3).
Expert Tips and Advice
1. Start with the basics: Ensure a strong foundation in the fundamental principles of polynomials and factoring.
2. Practice regularly: Engage in consistent practice to enhance your problem-solving skills and develop a deeper understanding of the concepts.
3. Seek guidance: Do not hesitate to seek assistance from teachers, mentors, or online resources if you encounter difficulties.
4. Stay curious: Explore various factoring techniques and delve into the applications of factoring in the real world.
Frequently Asked Questions
- Q: How do you determine if a polynomial has a leading coefficient of 1?
A: The leading coefficient is the coefficient of the term with the highest degree. If this coefficient is 1, then the polynomial has a leading coefficient of 1.
- Q: Why is it important to find the roots of a polynomial?
A: The roots of a polynomial are the values of the variable that make the polynomial equal to zero. Finding the roots is crucial for factoring the polynomial, as the polynomial can be expressed as a product of factors that are linear in terms of the roots.
In conclusion, factoring polynomials with a leading coefficient of 1 requires a combination of techniques, including simplification through combination, identifying the roots, and utilizing the substitution method. By understanding these methods, you can effectively factor complex polynomials and solve various algebraic equations with ease.
Are you eager to delve deeper into the fascinating world of polynomial factoring? Share your insights, ask questions, and let’s explore this mathematical concept together!
Explain How To Factor When The Leading Coefficient Is 1.
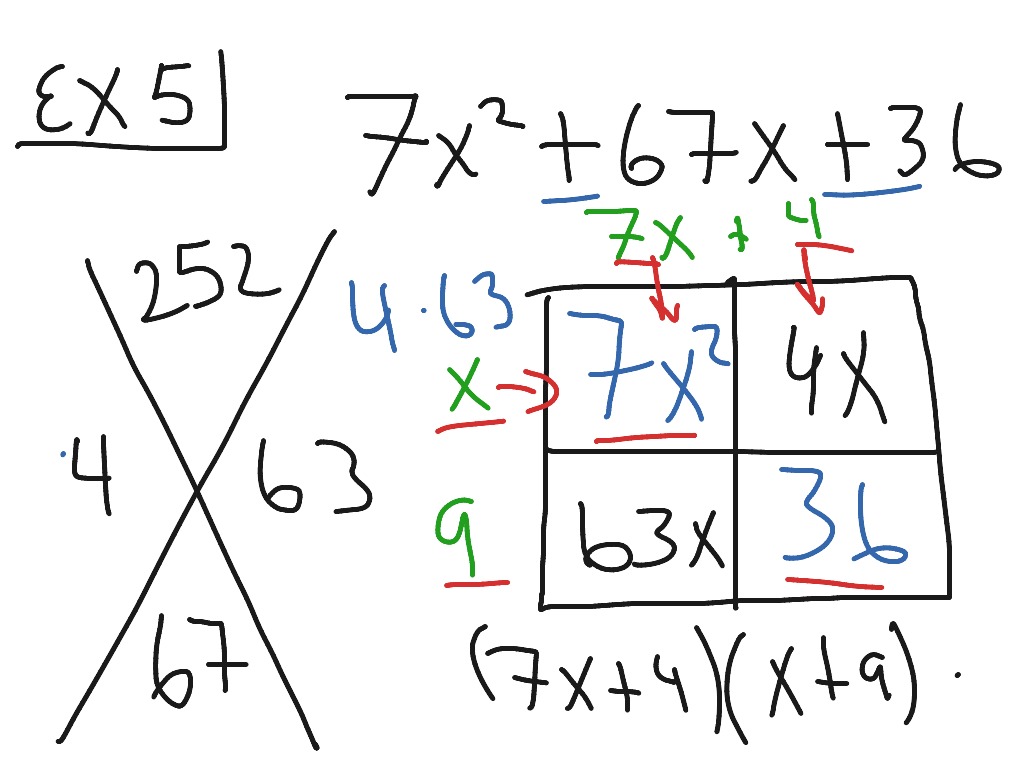
Image: www.showme.com
We express our gratitude for your visit to our site and for reading Explain How To Factor When The Leading Coefficient Is 1.. We hope this article is beneficial for you.